New Semiconductor Materials. Biology systems.
Characteristics and Properties

NSM Archive - Silicon Carbide (SiC) - Band structure

Band structure and carrier concentration

Basic Parameters
Band structure
Intrinsic carrier concentration
Effective Density of States in the Conduction and Valence Band
Temperature Dependences
Dependences on Hydrostatic Pressure
Energy Gap Narrowing at High Doping Levels
Effective Masses and Density of States
Donors and Acceptors

---

More than 200 different polytypes of SiC are known. However, about 95% of all publications deal with three main polytypes: 3C, 4H, and 6H. In all main polytypes of SiC, some atoms have been observed in association both with cubic (C), with hexagonal (H) and with rombohedral (R) lattice sites.

Basic Parameters

3C-SiC: cubic unit cell (Zincblende)		Remarks	Referens
Energy gaps, Egind(Γ15v -X1c)	2.416(1) eV	2 K, wevelength modulated absorption	Bimberg et al.(1981)
Energy gaps, Eg	2.36 eV	300 K	Goldberg et al.(2001)
Energy gaps, Egdir(Γ15v -X1c)	6.0 eV	300 K, optical absorption	Dalven (1965)
Excitonic Energy gaps, Egx	2.38807(3) eV	1.4 K, wevelength modulated absorption see also Temperature Dependences	Gorban' et al.(1984)

Conduction band		Remarks	Referens
Energy separation between  Γ15v valley and L1c valleys EL	4.6 eV	300 K	Goldberg et al.(2001)
Energy separation between  Γ15v valley and Γ1c valleys EΓ	6.0 eV	300 K
Valence band
Energy of spin-orbital splitting Eso	0.01 eV	300 K	Goldberg et al.(2001)
Energy of crystal-field splitting Ecr	---
Effective conduction band density of states	1.5 x 1019cm-3	300 K
Effective valence band density of states	1.2 x 1019 cm-3	300 K

2H-SiC: Hexagonal unit cell (Wurtzite)		Remarks	Referens
Excitonic Energy gaps, Eg	3.330 eV	optical absorption see also Temperature Dependences	Patrick et al.(1966)

4H-SiC: Hexagonal unit cell (Wurtzite)		Remarks	Referens
Energy gaps, Eg	3.23 eV	300 K	Goldberg et al.(2001)
Excitonic Energy gaps, Egx	3.20 eV	see also Temperature Dependences	Dubrovskii & Lepneva (1977)

Conduction band		Remarks	Referens
Energy separation between  Γ15v valley and L valleys EL	~=4. eV	300 K	Goldberg et al.(2001)
Energy separation between  Γ15v valley and Γ1c valleys EΓ	5-6.0 eV	300 K
Valence band
Energy of spin-orbital splitting Eso	0.007 eV	300 K	Goldberg et al.(2001)
Energy of crystal-field splitting Ecr	0.008 eV
Effective conduction band density of states	1.7 x 1019cm-3	300 K
Effective valence band density of states	2.5 x 1019 cm-3	300 K

6H-SiC: Hexagonal unit cell (Wurtzite)		Remarks	Referens
Energy gaps, Eg	3.0 eV	300 K	Goldberg et al.(2001)
Energy gaps, Egind	2.86 eV	300 K, optical absorption see also Temperature Dependences	Philipp & Taft (1960)
Excitonic Energy gaps, Eg	3.0230 eV	wevelength modulated absorption see also Temperature Dependences	Humphreys et al.(1981)

Conduction band		Remarks	Referens
Energy separation between  Γ15v valley and Γ1c valleys EΓ	5-6.0 eV	300 K	Goldberg et al.(2001)
Valence band
Energy of spin-orbital splitting Eso	0.007 eV	300 K	Goldberg et al.(2001)
Energy of crystal-field splitting Ecr	0.05 eV
Effective conduction band density of states	8.9 x 1019cm-3	300 K
Effective valence band density of states	2.5 x 1019 cm-3	300 K

8H-SiC: Hexagonal unit cell (Wurtzite)		Remarks	Referens
Excitonic Energy gaps, Eg	2.86 eV	see also Temperature Dependences	Dubrovskii & Lepneva (1977)

15R-SiC: Rhombohedral unit cell		Remarks	Referens
Excitonic Energy gaps, Eg	2.9863 eV	wevelength modulated absorption see also Temperature Dependences	Humphreys et al.(1981)

21R-SiC: Rhombohedral unit cell		Remarks	Referens
Excitonic Energy gaps, Eg	2.92 eV	see also Temperature Dependences	Dubrovskii & Lepneva (1977)

24R-SiC: Rhombohedral unit cell		Remarks	Referens
Excitonic Energy gaps, Eg	2.80 eV	see also Temperature Dependences	Dubrovskii & Lepneva (1977)

---

Band structure

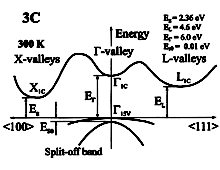	SiC, 3C. Band structure. Important minima of the conduction band and maxima of the valence band. .   300K;     Eg = 2.36 eV;       EΓ = 6.0 eV;     EL = 4.6 eV;     Eso = 0.01 eV.  For details see Persson & Lindefelt (1997)
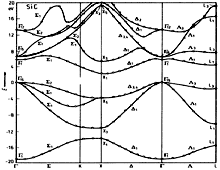	SiC, 3C. Band structure Hemstreet & Fong (1974)
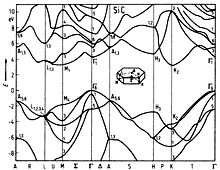	SiC, 2H. Band structure Hemstreet & Fong (1974)
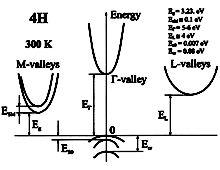	SiC, 4H. Band structure. Important minima of the conduction band and maxima of the valence band. .   300K;     Eg = 3.23 eV;       EΓ = 5-6.0 eV;     EL ~= 4.0 eV;     EsM ~= 0.1 eV.      Ecr = 0.08 eV;     Eso = 0.007 eV.  For details see Persson & Lindefelt (1997)
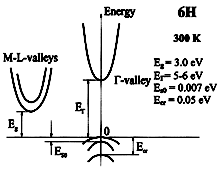	SiC, 4H. Band structure. Important minima of the conduction band and maxima of the valence band. .   300K;     Eg = 3.0 eV;       EΓ = 5 - 6.0 eV;     Ecr = 0.05 eV;     Eso = 0.007 eV.  For details see Persson & Lindefelt (1997)

In all polytypcs except 3C- and riH-Sif atomic hiyers wilh cubic (C) and hexagonal (H) symmetry follow in a regular alternation in the direct ion of the c axis. This can be thought of as anutural one-dimensional superkmice imposed on the "pure" i.e. h-layer free 3C-SiC [Dean et al. (1977)], the period of the superlattice being different for different modifications.

	Brillouin zone of the cubic lattice.
	Brillouin zone of the hexagonal lattice.

---

Temperature Dependences

Temperature dependence of energy gap:

3C-SiC	Eg = Eg(0) - 6.0 x 10-4 x T2/(T + 1200)	(eV)	Goldberg et al.(2001)
	Egx = 3.024-0.3055x10-4 +T2/(311K - T)	(eV)	Ravindra & Srivastava (1979)
4H-SiC	Eg = Eg(0) - 6.5 x 10-4 x T2/(T + 1300)		Goldberg et al.(2001)
6H-SiC	Eg = Eg(0) - 6.5 x 10-4 x T2/(T + 1200)

where T is temperature in degrees K.

	SiC, 3C, 4H, 6H. Energy gap vs. temperature. Choyke(1969)
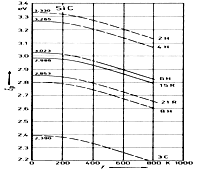	SiC, 3C, 15R, 21R, 2H, 4H, 6H, 8H. Excitonic energy gap vs. temperature Choyke(1969)
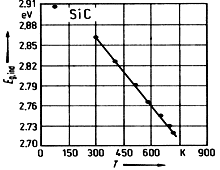
	SiC, 4H. Excitonic energy gap vs. temperature Choyke et al.(1964)
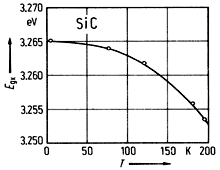
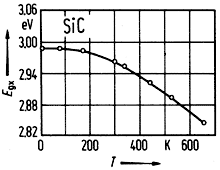
	SiC, 6H. Energy gap Egind vs. temperature Philipp & Taft(1960)
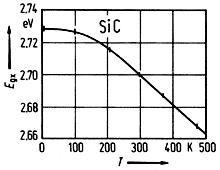
	SiC, 15R. Excitonic energy gap vs. temperature Patric et al. (1963)
	SiC, 24R. Excitonic energy gap vs. temperature Zanmarchi (1964)

---

Intrinsic carrier concentration:

n_i = (N_c·N_v)^1/2exp(-E_g/(2k_BT))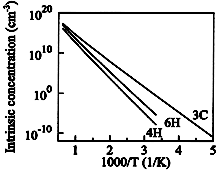

SiC, 3C, 4H, 6H. Intrinsic carrier concentration vs. temperature Goldberg et al.(2001)

see also Ruff et al. (1994), Casady and Johnson (1996).

Effective density of states in the conduction band N_c

3C-SiC

N_c ~= 4.82 x 10¹⁵ · M · (m_c/m₀)^3/2·T^3/2 (cm^-3) ~= 4.82 x 10¹⁵ (m_cd/m₀)^3/2·x T^3/2 ~= 3 x 10¹⁵ x T^3/2(cm^-3) ,
where M=3 is the number of equivalent valleys in the conduction band.
      m_c = 0.35m₀ is the effective mass of the density of states in one valley of conduction band.
      m_cd = 0.72 is the effective mass of density of states.

4H-SiC

N_c ~= 4.82 x 10¹⁵ · M · (m_c/m₀)^3/2·T^3/2 (cm^-3) ~= 4.82 x 10¹⁵ (m_cd/m₀)^3/2·x T^3/2 ~= 3.25 x 10¹⁵ x T^3/2(cm^-3) ,
where M=3 is the number of equivalent valleys in the conduction band.
      m_c = 0.37m₀ is the effective mass of the density of states in one valley of conduction band.
      m_cd = 0.77 is the effective mass of density of states.

6H-SiC

N_c ~= 4.82 x 10¹⁵ · M · (m_c/m₀)^3/2·T^3/2 (cm^-3) ~= 4.82 x 10¹⁵ (m_cd/m₀)^3/2·x T^3/2 ~= 1.73 x 10¹⁵ x T^3/2(cm^-3) ,
where M=6 is the number of equivalent valleys in the conduction band.
      m_c = 0.71m₀ is the effective mass of the density of states in one valley of conduction band.
      m_cd = 2.34 is the effective mass of density of states.

Effective density of states in the valence band N_v

3C-SiC	Nv = 2.23x1015 x T3/2 (cm-3)	Ruff et al. (1994), Casady and Johnson (1996)
4H-SiC	Nv ~= 4.8x1015 x T3/2 (cm-3)
6H-SiC	Nv ~= 4.8x1015 x T3/2 (cm-3)

---

Dependence on Hydrostatic Pressure

3C-SiC	Eg = Eg(0) - 0.34 x 10-3P	(eV)	Park et al. (1994)
	EL = EL(0) + 3.92 x 10-3P	(eV)
	EΓ = EΓ(0) + 5.11 x 10-3P	(eV)
4H-SiC	Eg = Eg(0) + 0.8 x 10-3P	(eV)
	EΓ = EΓ(0) + 3.7 x 10-3P	(eV)
6H-SiC	Eg = Eg(0) - 0.03 x 10-3P	(eV)
	EΓ = EΓ(0) + 4.03 x 10-3P	(eV)

here P is pressure in kbar Park et al. (1994).

---

Energy Gap Narrowing at High Doping Levels:

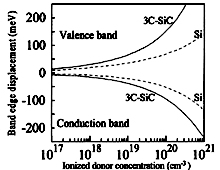	3C-SiC. Conduction and valence band displacements vs. ionized shallow impurity. n-type material. For comparison, the band-edge displacements for Si are shown Lindefelt (1998)
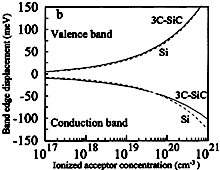	3C-SiC. Conduction and valence band displacements vs. ionized shallow impurity. p-type material. For comparison, the band-edge displacements for Si are shown Lindefelt (1998)
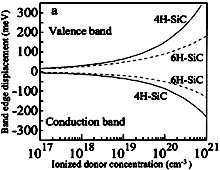	4H-SiC, 6H-SiC. Conduction and valence band displacements vs. ionized shallow impurity. n-type material. For comparison, the band-edge displacements for Si are shown Lindefelt (1998)
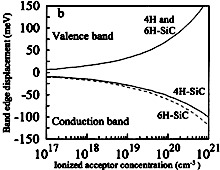	4H-SiC, 6H-SiC. Conduction and valence band displacements vs. ionized shallow impurity. p-type material. For comparison, the band-edge displacements for Si are shown Lindefelt (1998)

The band-edge displacements for n-type material Lindefelt (1998) :
ΔE_nc=A_nc(N_D⁺)^1/3 x 10^-6 + B_nc(N_D⁺)^1/2 x 10^-9 (eV)
ΔE_nv=A_nv(N_D⁺)^1/3 x 10^-6 + B_nv(N_D⁺)^1/2 x 10^-9 (eV)
where

n-type	Anc	Bnc	Anv	Bnv
Si	-9.74x10-3	-1.39x10-3	-1.27x10-2	-1.40x10-3
3C-SiC	-1.48x10-2	-3.06x10-3	-1.75x10-2	-6.85x10-3
4C-SiC	-1.50x10-2	-2.93x10-3	-1.90x10-2	-8.74x10-3
6C-SiC	-1.12x10-2	-1.01x10-3	-2.11x10-2	-1.73x10-3

The band-edge displacements for p-type material Lindefelt (1998) :
ΔE_pc=A_pc(N_D⁺)^1/3 x 10^-6 + B_pc(N_D⁺)^1/2 x 10^-9 (eV)
ΔE_pv=A_pv(N_D⁺)^1/3 x 10^-6 + B_pv(N_D⁺)^1/2 x 10^-9 (eV)
where

p-type	Apc	Bpc	Apv	Bpv
Si	-1.14x10-3	-2.05x10-3	-1.11x10-2	-2.06x10-3
3C-SiC	-1.50x10-2	-6.41x10-4	-1.30x10-2	-1.43x10-3
4C-SiC	-1.57x10-2	-3.87x10-4	-1.30x10-2	-1.15x10-3
6C-SiC	-1.74x10-2	-6.64x10-4	-1.30x10-2	-1.14x10-3

---

Effective Masses and Density of States:

Electrons

3C-SiC. The surfaces of equal energy are ellipsoids:

3C-SiC		Remarks	Referens
Effective electron mass       (longitudinal)ml	0.68mo		Son et al. (1994); Son et al. (1995)
	0.677(15)mo	45K, Cyclotrone resonance	Kaplan et al. (1985)
Effective electron mass       (transverse)mt	0.25mo		Son et al. (1994); Son et al. (1995)
	0.247(11)mo	45K, Cyclotrone resonance	Kaplan et al. (1985)
Effective mass of density of states  mcd	0.72mo		Son et al. (1994); Son et al. (1995)
Effective mass of the density of states in one valley of conduction band mc	0.35mo
Effective mass of conductivity  mcc	0.32mo

There are 3 equivalent valleys in conduction band

4H-SiC. The surfaces of equal energy are ellipsoids:

4H-SiC		Remarks	Referens
Effective electron mass       (longitudinal)ml	0.29mo		Son et al. (1994); Son et al. (1995)
Effective electron mass       (transverse)mt	0.42mo		Son et al. (1994); Son et al. (1995)
Effective mass of density of states  mcd	0.77mo		Son et al. (1994); Son et al. (1995)
Effective mass of the density of states in one valley of conduction band mc	0.37mo
Effective mass of conductivity  mcc	0.36mo

There are 3 equivalent valleys in conduction band

6H-SiC. The surfaces of equal energy are ellipsoids:

6H-SiC		Remarks	Referens
Effective electron mass       (longitudinal)ml	0.20mo		Son et al. (1994); Son et al. (1995)
Effective electron mass       (transverse)mt	0.42mo		Son et al. (1994); Son et al. (1995)
Effective mass of density of states  mcd	2.34mo		Son et al. (1994); Son et al. (1995)
Effective mass of the density of states in one valley of conduction band mc	0.71mo
Effective mass of conductivity  mcc	0.57mo

There are 6 equivalent valleys in conduction band

Holes

Due to the small spin-orbit splitting the valence bands are highly non-parabolic, i.e. effective hole masses become strongly k-dependent.

SiC			Remarks	Referens
3C	Effective mass of density of state mv   Statistics