New Semiconductor Materials. Biology systems.
Characteristics and Properties

Electrical properties of Germanium (Ge)

Electrical properties

Basic Parameters
Mobility and Hall Effect
Transport Properties in High Electric Fields
Impact Ionization
Recombination Parameters

Basic Parameters

Breakdown field	≈105V cm-1
Mobility electrons	≤3900 cm2 V-1s-1
Mobility holes	≤1900 cm2 V-1s-1
Diffusion coefficient electrons	≤100 cm2 s-1
Diffusion coefficient holes	≤50 cm2 s-1
Electron thermal velocity	3.1·105m s-1
Hole thermal velocity	1.9·105m s-1

Mobility and Hall Effect

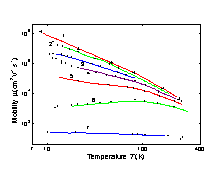Electron mobility versus temperature for different doping levels. 1. High purity Ge; time-of-flight technique (Jacoboni et al. [1981]); 2-6. Hall effect Nd - Na(cm-3): 2. 1·1013; 3. 1.4·1014; 4. 1.7·1015; 5. 7.5·1015; 6. 5.5·1016 (Debye and Conwell [1954]); 7. Hall effect Nd - Na=1.2·1019(cm-3) (Fistul et al. [1962]).

For weakly doped Ge in the range 77-300 K electron mobility
µ_n≈ 4.9·10⁷·T^-1.66 (cm² V^-1 s^-1).

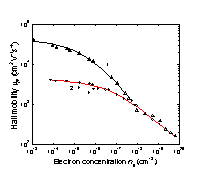Electron Hall mobility versus electron concentration 1. T = 77 K; 2. T = 300 K. (Fistul et al. [1962]).

Approximate formula for the Hall mobility. 300 K.

µ_n=µ_OH/(1+N_d·10^-17)^1/2,
where µ_OH≈=3900 (cm² V^-1 s^-1),
N_d- in cm^-3
(Hilsum [1974]).

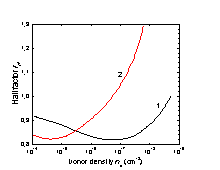	The electron Hall factor versus donor density. 1. T = 300 K; 2. T = 77 K. (Babich et al. [1969]).
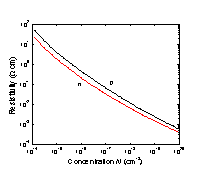	Resistivity versus impurity concentration., T = 300 K. (Cuttris [1981]).
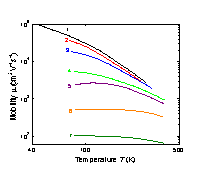	Temperature dependences of hole mobility for different doping levels. 1. High purity Ge; time-of-flight technique (Ottaviany et al. [1973]). 2-7. Hall-effect (Golikova et al. [1961]). Na- Nd (cm-3): 2. = 4.9·1013; 3. 3.2·1015; 4. 2.7·1016; 5. 1.2·1017; 6. 4.9·1018; 7. 2.0·1020.

For weakly doped Ge in the range 100-300 K hole mobility
µ_p≈1.05·10⁹·T^-2.33 (cm² V^-1 s^-1)

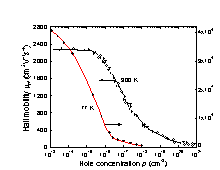	The hole Hall mobility versus hole concentration. Experimental points: data from three References (Golikova et al. [1961]).
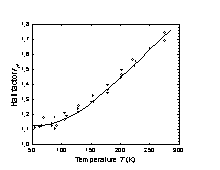	The hole Hall factor versus temperature for high purity p-Ge (Morin [1954]).

Transport Properties in High Electric Fields

	Ge. Electron drift velocity vs. electric field. Solid lines: F||(100) Solid lines: F||(111). Jacoboni et al. (1981).
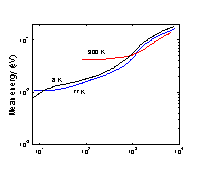	Ge. Mean energy of electrons in lower valleys vs. electronic field for three lattice temperatures. (Jacoboni et al. [1981]). (Jacoboni et al. [1981]).
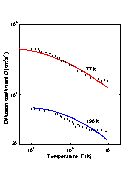	Ge. Longitudinal electron diffusion coefficient D vs. electric field for 77 K and 190 K. F||(100). Solid lines show the results calculation. Symbols represent measured data. (Jacoboni et al. [1981]).
	Ge. Electron drift velocity vs. electric field at different temperatures. F||(100). Ottaviani et al. (1973).
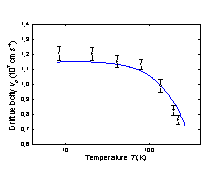	Ge. Drift velocity Vd vs. of temperature for electric field F=104(V cm-1). F||(100). Solid line show the results of calculation in the case where non-parabolic effect are taken into account (Reggiani et al. [1977]).
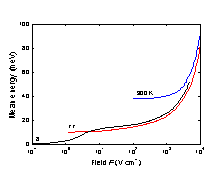	Ge. Mean energy of hole vs. electronic field F at different lattice temperatures. Solid line are Monte-Carlo calculations for F||(111) (Reggiani et al. [1977]). Points show experimental results for 82 K. (Vorob'ev et al. [1978]).
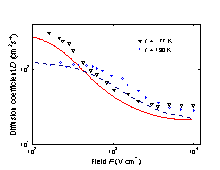	Ge. Longitudinal hole diffusion coefficient D vs. electronic field for 77 K and 190 K. F||(111). Dashed and solid lines show the results of the calculations. Symbols represent measured data. (Reggiani et al. [1978]).

Impact Ionization

There are two schools of thought regarding the impact ionization in Ge.

The first one states that impact ionization rates α_i and β_i for electrons and holes in Ge are known accurately enough to distinguish such subtle details as the anisothropy of α_i and β_i for different crystallographic directions.

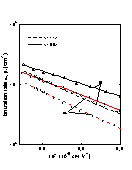Ionization rates in (111) and (100) directions versus 1/F. T = 300 K. (Mikava et al. [1977]).

			Remarks	Referens
Electron ionization rates	Ge (111)	αi = α0 x exp(-Ei /E), where α0 = 2.72x106 1/cm, Ei = 1.1x106 V/cm	(111), 300 K	Mikava et al. (1980)
	Ge (100)	αi = α0 x exp(-Ei /E), where α0 = 8.04x106 1/cm, Ei = 1.4x106 V/cm	(100), 300 K	Mikava et al. (1980)
Hole ionization rates	Ge (111)	βi = β0 x exp(-Ei /E), where β0 = 1.72 x 106 1/cm, Ei = 9.37 x 105 V/cm	(111), 300 K	Mikava et al. (1980)
	Ge (100)	βi = β0 x exp(-Ei /E), where β0 = 6.39 x 106 1/cm, Ei = 1.27 x 106 V/cm	(100), 300 K	Mikava et al. (1980)

The second school contends that the values of α_i and β_i for the same electric field reported by different researches differ by an order of magnitude. This point of view is explained by Kyuregyan and Yurkov [1989]. In accordance with this approach we can assume for all crystallographic directions that

For electrons: αi=αoexp(-Fno/ F)
where	αo = 2.84·106 cm-1	Fno = 1.14·106 V cm-1
For holes: βi=βoexp(-Fpo/ F)
where	βo = 4.21·106 cm-1	Fpo = 1.11·106 V cm-1

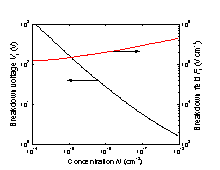Breakdown voltage and breakdown field versus doping density for an abrupt p-n junction. (Kyuregyan and Yurkov [1989]).

Recombination Parameters

Pure n-type material
300 K
The longest lifetime of holes	τp≥ 10-3 s
Diffusion length	Lp≥ 0.2 cm
77 K
The longest lifetime of holes	τp≥ 10-4 s
Diffusion length	Lp≥ 0.15 cm
Pure p-type material
300 K
The longest lifetime of electrons	τn≥ 10-3 s
Diffusion length	Ln≥ 0.3 cm
77 K
The longest lifetime of electrons	τn≥ 10-4 s
Diffusion length	Ln≥ 0.15 cm
Surface recombination	10 ÷ 106cm/s.
Radiative recombination coefficient at 300 K	6.41·10-14 cm3 s-1
Auger coefficient at 300 K	~10-30 cm6 s-1

SiGe			Remarks	Referens
	The longest lifetime of holes tp	x 10-7 c	300 K
	Diffusion length Lp = (Dp x tp)1/2	μm c
	Surface Recombinaton Velocity	1
	Radiative recombination coefficient B	x 10-12 cm3/s
	Auger coefficient Cn	x 10-31 cm6/s
	Auger coefficient Cp	x 10-31 cm6/s
	Auger coefficient C = Cn + Cp	x 10-31 cm6/s

 

Statistics