New Semiconductor Materials. Biology systems.
Characteristics and Properties

Band structure and carrier concentration of Gallium Antimonide (GaSb)

Band structure and carrier concentration

Basic Parameters
Temperature Dependences
Dependence of the Energy Gap on Hydrostatic Pressure
Energy Gap Narrowing at High Doping Levels
Effective Masses
Donors and Acceptors

Basic Parameters

Energy gap	0.726 eV
Energy separation (EΓL) between Γ and L valleys	0.084 eV
Energy separation (EΓX) between Γ and X valleys	0.31 eV
Energy spin-orbital splitting	0.80 eV
Intrinsic carrier concentration	1.5·1012 cm-3
Intrinsic resistivity	103 Ω·cm
Effective conduction band density of states	2.1·1017 cm-3
Effective valence band density of states	1.8·1019 cm-3

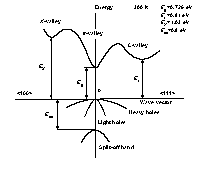Band structure and carrier concentration of GaSb. 300 K Eg= 0.726 eV EL = 0.81 eV EX = 1.03 eV Eso = 0.8 eV

Temperature Dependences

Temperature dependence of the energy gap
(Wu and Chen [1992])

E_g = 0.813 - 3.78·10^-4·T²/(T+94) (eV),
where T is temperature in degrees K (0 < T < 300).

Temperature dependence of energy E_L

E_L = 0.902 - 3.97·10^-4·T²/(T+94) (eV)

Temperature dependence of energy E_X
(Lee and Woolley [1981])

E_X = 1.142 - 4.75·10^-4·T²/(T+94) (eV)

Effective density of states in the conduction band

N_c = 4.0·10¹³·T^3/2 (cm^-3)

Effective density of states in the conduction band

N_c = 4.0·10¹³·T^3/2 (cm^-3)

Effective density of states in the valence band

N_v = 3.5·10¹⁵·T^3/2 (cm^-3)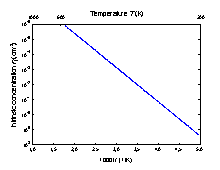

The temperature dependences of the intrinsic carrier concentration.

Dependences on Hydrostatic Pressure

E_g = E_g(0) + 14.5·10^-3P (eV)
E_L = E_L(0) + 5.0·10^-3P (eV)
E_X = E_X(0) - 1.5·10^-3P (eV),
where P is pressure in kbar.

Energy Gap Narrowing at High Doping Levels

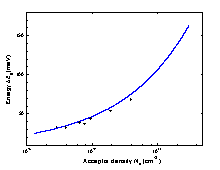Energy gap narrowing versus acceptor acceptor doping density. Curve is calculated for p-GaSb according to Jain et al. [1990]. Points show experimental results (Titkov et al. [1981]).

For n-type GaSb
(Jain et al. [1990]):

E_g = 13.6·10^-9·N_d^1/3 + 1.66·10^-7·N_d^1/4 + 119·10^-12·N_d^1/2 (eV)

For p-type GaSb
(Jain et al. [1990]):

E_g = 8.07·10^-9·N_a^1/3 + 2.80·10^-7·N_a^1/4+ 4.12·10^-12·N_a^1/2 (eV)

Effective Masses

Electrons:

For Γ-valley	mΓ = 0.041mo
In the L- valley the surfaces of equal energy are ellipsoids
	ml= 0.95mo
	mt= 0.11mo
Effective mass of density of states
	mL= 16(mlmt2)1/3= 0.57mo
In the X- valley the surfaces of equal energy are ellipsoids
	ml= 1.51mo
	mt= 0.22mo
Effective mass of density of states
	mX= 9(mlmt2)1/3= 0.87mo

Holes:

Heavy	mh = 0.4mo
Light	mlp = 0.05mo
Split-off band	mso = 0.14mo
Effective mass of density of states	mv = 0.8mo
Effective mass of density of conductivity (Heller and Hamerly [1985])	mvc = 0.3mo

Donors and Acceptors

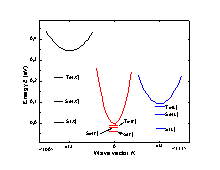
The diagram of IV group donor states (Vul' et al. [1970]).

Ionization energies of shallow donors (eV)

Te(L)	Te(X)	Se(L)	Se(X)	S(L)	S(X)
~0.02	≤0.08	~0.05	~0.23	~0.15	~0.30

For typical donor concentrations N_d≥ 10¹⁷ cm^-3 the shallow donor states connected with Γ-valley did not appear.

Ionization energies of shallow acceptors (eV):

The dominant acceptor of undoped GaSb seems to be a native defect.
This acceptor is doubly ionizable

Ea1	Ea2	Si	Ge	Zn
0.03	0.1	~0.01	~0.009	~0.037

 

Statistics