NSM Archive - Gallium Nitride (GaN) - Band structure
Band structure and carrier concentration
Basic Parametersfor Zinc Blende crystal structure
for Wurtzite crystal structure
Band structure
for Zinc Blende crystal structure
for Wurtzite crystal structure
Intrinsic carrier concentration
Effective Density of States in the Conduction and Valence Band
Temperature Dependences
Dependences on Hydrostatic Pressure
Band Discontinuities at Heterointerfaces
Effective Masses and Density of States
Donors and Acceptors
The Most Important Levels
Basic Parameters
Zinc Blende crystal structure
| Remarks | Referens | ||
| Energy gaps, Eg |
3.28 eV | 0 K | Bougrov et al. (2001) | Energy gaps, Eg |
3.2 eV | 300 K |
| Electron affinity | 4.1 eV | 300 K | |
| Conduction band | |||
| Energy separation between Γ valley and X valleys EΓ | 1.4 eV | 300 K | Bougrov et al. (2001) |
| Energy separation between Γ valley and L valleys EL | 1.6 ÷ 1.9 eV | 300 K | |
| Effective conduction band density of states | 1.2 x 1018 cm-3 | 300 K | |
| Valence band | |||
| Energy of spin-orbital splitting Eso |
0.02 eV |
300 K | |
| Effective valence band density of states | 4.1 x 1019 cm-3 | 300 K |
Wurtzite crystal structure
| Remarks | Referens | ||
| Energy gaps, Eg | 3.47 eV | 0 K | Bougrov et al. (2001) |
| 3.39 eV | 300 K | Chow & Ghezzo (1996) | |
| Energy gaps, Eg,dir | 3.503 (2) eV | 1.6 K; photoluminescence, from excitonic gap adding the exciton binding energy |
Monemar (1974) |
| 3.4751(5) eV | 1.6 K; A-exciton (transition from Γ9v) | ||
| 3.4815(10) eV | 1.6 K; B-exciton (transition from upper Γ7v) | ||
| 3.493 (5) eV | 1.6 K; C-exciton (transition from lower Γ7v) | ||
| 3.44 eV | 300K; temperature dependence below 295 K given by: Eg(T) - Eg(0) = - 5.08 x 10-4 T2/(996 - T), (T in K) . see also Figure "Band gap energy and exciton energies vs. temperature" |
Madelung (1991) | |
| Electron affinity | 4.1 eV | 300 K | Bougrov et al. (2001) |
| Remarks | Referens | ||
| Conduction band | |
||
| Energy separation between Γ valley and M-L valleys | 1.1 ÷ 1.9 eV | 300 K | Bougrov et al. (2001) |
| Energy separation between M-L-valleys degeneracy | 6 eV | 300 K | |
| Energy separation between Γ valley and A valleys | 1.3 ÷ 2.1 eV | 300 K | |
| Energy separation between A-valley degeneracy |
1 eV |
300 K | |
| also The energy separations between the Γ9
state and the two Γ 7 states can be calculated from the energy separations of the A-, B-, C-excitons. |
Madelung (1991) | ||
| Effective conduction band density of states | 2.3 x 1018 cm-3 | 300 K | |
| Valence band | |||
| Energy of spin-orbital splitting Eso | 0.008 eV | 300 K | Bougrov et al. (2001) |
| Energy of spin-orbital splitting Eso | 11(+5,-2) meV | 300 K; calculated from the values of energy gap Eg,dir (given above) |
Dingle & Ilegems (1971) |
|
Energy of crystal-field splitting Ecr |
0.04 eV | 300 K | Bougrov et al. (2001) |
|
Energy of crystal-field splitting Ecr |
22(2) meV | 300 K; calculated from the values of energy gap Eg,dir (given above) |
Dingle & Ilegems (1971) |
|
Effective valence band density of states |
4.6 x 1019 cm-3 | 300 K | |
Band structure for Zinc Blende GaN
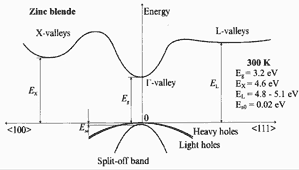 |
Band structure of zinc blende(cubic) GaN. Important minima of the
conduction band and maxima of the valence band. 300K; Eg =3.2 eV eV; EX= 4.6 eV; EL= 4.8-5.1 eV; Eso = 0.02 eV For details see Suzuki, Uenoyama & Yanase (1995) . |
 |
Brillouin zone of the face centered cubic lattice, the Bravais lattice of the diamond and zincblende structures. |
Band structure for Wurtzite GaN
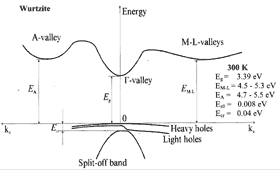 |
GaN, Wurtzite. Band structure. Important minima of
the conduction band and maxima of the valence band. Valence band 3 splitted
bands. This splitting results from spin-orbit interaction and from crystal
symmetry. 300K; Eg =3.39 eV eV; EM-L= 4.5-5.3 eV; EA= 4.7-5.5 eV; Eso = 0.008 eV; Ecr = 0.04 eV For details see Suzuki, Uenoyama & Yanase (1995) . |
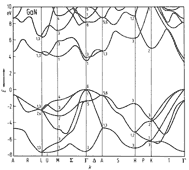 |
GaN, Wurtzite. Band structure calculated with an empirical
pseudopotential method The band structure differs only slightly from other spin-neglecting calculations. Introduction of spin-orbit interaction leads to a splitting of the uppermost valence band at Γ from Γ1 + Γ6 , into Γ9 + Γ7 + Γ7 . The energy differences between these terms can be described by two parameters - the spin-orbit splitting energy Eso (Δso) and the crystal field splitting energy Ecr(Δcr). Also see Basic Parameters. Bloom et al.(1974) |
 |
Brillouin zone of the hexagonal lattice. |
Temperature Dependences
The energy gap versus temperature:| Eg = Eg(0) - 7.7·10-4x
T2/(T + 600) |
(eV) | Bougrov et al. (2001 |
| Eg(0) = 3.47 eV (wurtzite)
Eg(0) = 3.28 eV (zinc blende) |
||
| Eg = Eg(0) - 9.39 x 10-4
x T2/(T + 772) |
(eV) | Guo & Yoshida (1994) Teisseyre al. (1994) |
| Eg (0 K) = 3.427 eV |
| Varshni expression: | ||
| Eg = Eg(0) - 9.39·10-4x T2/(T + 772) | (eV) | Guo & Yoshida (1994),
Teisseyre al. (1994) |
| where Eg(0) = 3.427 eV and T is temperature in degrees K |
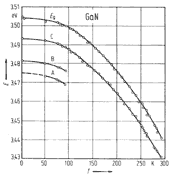 |
GaN, Wurtzite. Band gap energy and exciton energies vs. temperature Monemar (1974) Temperature dependence below 295 K given by: Eg(T) - Eg(0) = - 5.08 x 10-4 T2/(996 - T), (T in K). Eg(300K) =3.44 eV |
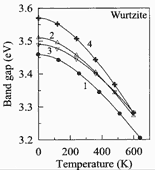 |
GaN, Wurtzite. Band gap energy versus temperature. GaN samples
were grown on different substrates using different techniques. Experimental
data are taken from four different works. Bougrov et al. (2001) |
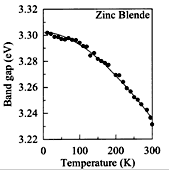 |
GaN, Zinc Blende(cubic). The Band gap energy versus temperature.
GaN films were grown on MgO (1x1) substrates. Ramirez-Flores et al. (1994) |
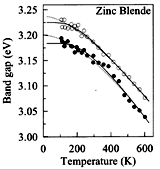 |
GaN, Zinc Blende(cubic). The Band gap energy versus temperature.
GaN films were grown on Si (100) substrates. The dependences were extracted
from pseudodielectric-function spectrum using two different theoretical
models Petalas et al. (1995) |
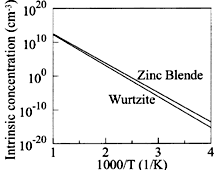 |
GaN, Wurtzite & Zinc Blende. The intrinsic carrier concentration
vs. temperature. Bougrov et al. (2001) |