NSM Archive - Gallium Indium Arsenide GaInAs) - Band structure

Band structure and carrier concentration
Basic ParametersBand structure
Intrinsic carrier concentration
Lasing wavelength
Effective Density of States in the Conduction and Valence Band
Temperature Dependences
Dependences on Hydrostatic Pressure
Band Discontinuities at Heterointerfaces
Energy gap narrowing at high doping levels
Effective Masses and Density of States
Donors and Acceptors
Basic Parameters for GaxIn1-xAsyP1-y
Zinc Blende crystal structure
| Ga0.47In0.53As | GaxIn1-xAs | Remarks | Referens | |
| Energy gaps, Eg |
0.74 eV | (0.36+0.63x+0.43x2) eV | 300 K | Goetz et al.(1983) |
| Energy gaps, Eg |
(0.4105+0.6337x+0.475x2) eV | 2 K | Goetz et al.(1983) | |
| Electron affinity | 4.5 eV | (4.9-0.83x) eV | 300 K | |
| Conduction band | ||||
| Energy separation between X valley and top of the valence band EX |
1.33 eV | (1.37-0.63x+1.16x2) eV | 300 K | Goetz et al.(1983) |
| Energy separation between L valley and top of the valence band EL |
1.2 eV | (1.08-0.02x+0.65x2) eV | 300 K | Goetz et al.(1983) |
| Effective conduction band density of states | 2.1·1017 cm-3 | see Temerature dependences | ||
| Valence band | ||||
| Energy separation of spin-orbital splitting Eso | *** | *** | ||
| Effective valence band density of states | 7.7·1018 cm-3 | see Temerature dependences | ||
| Intrinsic carrier concentration | 6.3·1011 cm-3 | see Temerature dependences | ||
Band structure for GaxIn1-xAs
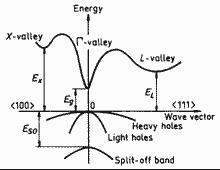 |
GaxIn1-xAs (zinc blende, cubic). Band structure
Important minima of the conduction band and maxima of the valence band.. For details see Goldberg Yu.A. & N.M. Schmidt (1999) . |
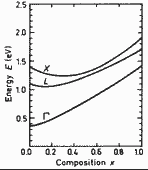 |
GaxIn1-xAs. Energy gap Eg Energy
separations between Γ- ,X-, and L -conduction band minima and top
of the valence band vs. composition parameter x. Porod and Ferry (1983) |
Interfacial elastic strain induced by lattice parameter mismatch between epilayer and substrate results in significant band-gap shifts:
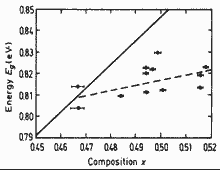 |
GaxIn1-xAs. Energy band gap Eg of unstrained
(solid line) and strained (dashed line and experimental points) vs. composition
parameter x. Solid line is calculated according to Eg= (0.4105+0.6337x+0.475x2) eV. Experimental points are obtained at 4K. Kuo et al.(1985) |
 |
Brillouin zone of the face centered cubic lattice, the Bravais lattice of the diamond and zincblende structures. |
 |
Brillouin zone of the hexagonal lattice. |
Temperature Dependences
| Eg (x,T)= 0.42 + 0.625x -[5.8/(T+300)-4.19
/(T+271)]·10-4T2x- - 4.19·10-4T2/(T+271) +0.475x2 (eV) |
(eV) | GaxIn1-xAs | Paul et al.(1991) | |
| Eg (x,T)= Eg (0) + (6x2-
8.6x +5.2)·10-4 T2/(337x2-
455x +196) |
GaxIn1-xAs on Ga As | Karachevtseva et al.(1994) | ||
| Eg (x,T)= 0.42 + 0.625x -[5.8/(T+300)-4.19
/(T+271)]·10-4T2x- - 4.19·10-4T2/(T+271) +0.475x2 (eV) |
(eV) | GaxIn1-xAs | ||
| where T is temperature in degrees K |
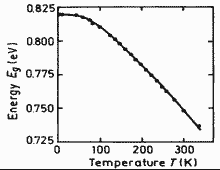 |
Ga0.47In0.53As. Energy gap Eg of vs. temperature Points are experimental data. Solid line is theoretical calculation. Eg(0)=821.5 ± 0.2 meV. Zielinski et al.(1986) |
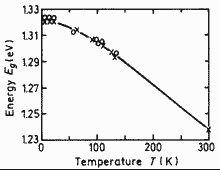 |
Ga0.87In0.13As. Energy gap Eg of vs. temperature Points are experimental data. Solid line -- 1.321 - 4.1·10-4 T2/(T+139) Karachevtseva et al.(1994) |
Lasing wavelength λ0
Intrinsic carrier concentration:
ni = (Nc·Nv)1/2exp(-Eg/(2kBT)) ~= 4.82 x 1015 · [(0.41-0.09x)3/2 +(0.027+0.047x)3/2]1/2 xx(0.025+0.043x)3/4[ T3/2 exp(-ν/2)(1+3.75/ν +3.28/ν2 -2.46/ν3)1/2 ] (cm-3) ,
where ν=E(x,T)/2kT
Paul et al.(1991).
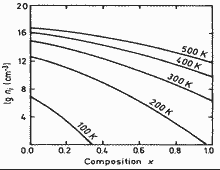 |
GaxIn1-xAs. Intrinsic carrier concentration
vs. temperature for GaxIn1-xAs. T = 100K; 200K; 300K; 400K; 500K; Paul et al.(1991) |
Effective density of states in the conduction band: Nc
Nc ~= 4.82 x 1015 · (mΓ/m0)3/2T3/2 (cm-3) ~= 4.82 x 1015 · (0.023+0.037x+0.003x2)3/2 T3/2 (cm-3) :Effective density of states in the valence band: Nv
Nv ~= 4.82 x 1015 · (mh/m0)3/2 T3/2 (cm-3)= 4.82 x 1015 · (0.41-0.1x)3/2 T3/2 (cm-3) :Dependence on Hydrostatic Pressure
| Eg (0.47,P)~= (0.796+10.9x 10-3 ·P -30x10-6 ·P2) eV | 80K, Ga0.47In0.53As | x=0.47 | Lambkin and Dunstan (1988) |
| Eg (0.47,P)~= (0.733+11.0x 10-3 ·P -27x10-6 ·P2) eV | 300K, Ga0.47In0.53As | x=0.47 | |
| Eg (0.0, P)~= (Eg (0)+4.8x 10-3 ·P) eV | 300K, InAs | x=0. | |
| Eg (1.0, P)~= (Eg (0)+12.6x 10-3 ·P -37.7x10-6 ·P2) eV | 300K, GaAs | x=1. |
Energy gap narrowing at high doping levels
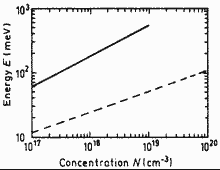 |
Ga0.47In0.53As. Energy gap narrowing Eg vs.
donor (solid line) and acceptor (dashed
line) doping density solid line -- donor doping density; dashed line -- acceptor doping density Jain et al. (1990) |
| ΔEg ~= (A ·N1/3 10-9 +B ·N1/4 10-7 +C ·N1/2 10-12) meV | 300K, Ga0.47In0.53As | x=0.47 | |
| where | |||
| n : A=15.5; B=1.95; C=159 | 300K, Ga0.47In0.53As | x=0.47 | |
| p : A= 9.2; B=3.57; C=3.65 | 300K, Ga0.47In0.53As | x=0.47 | |
| N -- carrier concentration in cm-3 |
Band Discontinuities at Heterointerfaces
Band discontinuities at GaxIn1-xAs/AlyGa1-yAs heterointerface Shur (1990).| Referens | ||||||
| Conduction band discontinuity | ΔEv =(ΔEg -ΔEv) eV | Shur (1990) | ||||
| Valence band discontinuity | ΔEc = (0.44 ΔEgg) eV | Shur (1990) | ||||
| where ΔEgg
(eV) = [1.247y + 1.5(1-x) - 0.4(1-x)2] (eV)
is the difference between Γ-valleys in GaxIn1-xAs and AlyGA1-yAs . |
||||||
| Energy gap Eg discontinuity : | ΔEg = ΔEgg | for y<0.45 | ||||
| Energy gap Eg discontinuity : | ΔEg = 0.476 +0.125y + 0.143y2 +1.5(1-x) - 0.4(1-x)2 | for y>0.45 | ||||
| Band discontinuities | ΔEv ~= 0.38 eV ΔEc ~= 0.22 eV |
at Ga0.47In0.53As/InP heterointerface |
Adachi (1992); Hybertsen (1991) |
|||
| Band discontinuities | ΔEv ~= 0.2 eV ΔEc ~= 0.52 eV |
at Ga0.47In0.53As/Al0.48In0.52As heterointerface |
Adachi (1992); Hybertsen (1991) |
|||
| ΔEc /ΔEg = [0.653 + 0.1(1-x)] eV | at GaxIn1-xAs/AlxIn1-xAs
heterointerface |
Wolak et al.(1991) | ||||
Effective Masses and Density of States:
Electrons
For wurtzite crystal structure the surfaces of equal energy in Γ valley should be ellipsoids, but effective masses in z direction and perpendicular directions are estimated to be approximately the same:| Effective Electron Masses | Remarks | Referens | |
| Effective electron mass me= mΓ | 0.023 -0.037x +0.003x2 mo | GaxIn1-xAs; 300K; for Γ - valley |
Goldberg Yu.A. & N.M. Schmidt (1999) |
| Effective electron mass me | mΓ= 0.041 mo at n= 2x·1017
cm-3 mΓ= 0.074 mo at n= 6x·1018 cm-3 |
Ga0.47In0.53As; x=0.47 |
Pearsall (1982) |
| mL = 0.29 mo ; ( L - valley ) mX = 0.68 mo ; ( X - valley ) |
Ga0.47In0.53As; x=0.47 |
Pearsall (1982) |
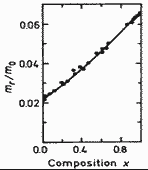 |
GaxIn1-xAs. Electron effective mass vs. concentration
x for GaxIn1-xAs; 300K Adachi (1992) |
Holes
| Effective Masses for Zinc Blende GaN | Remarks | Referens | |
| Effective hole masses (heavy) mh | mh ~= (0.41 -0.1x) mo | GaxIn1-xAs; 300K; | Goldberg Yu.A. & N.M. Schmidt (1999) |
| Effective hole masses (light) mlp | mlp ~= (0.026 -0.056x ) mo
|
GaxIn1-xAs; 300K; | |
| Effective hole masses (split-off band) ms | mso ~= 0.15 mo | GaxIn1-xAs; 300K; |
Donors and Acceptors
| Ionization energies of Shallow Donors |
Remarks | |||
| Sn, Ge, Si, C |
~ 5 meV |
Ga0.47In0.53As; x=0.47 |
Goldberg Yu.A. & N.M. Schmidt (1999) | |
| Sn, Ge, Si, S, Se, Te |
> 1 meV |
InAs; x=0 | ||
| Sn, Ge, Si, S, Se, Te |
~ 6 meV |
GaAs; x=1 | ||
| Ionization energies of Shallow Acceptor |
||||
| Mg |
~ 25 meV |
Ga0.47In0.53As; x=0.47 |
Goldberg Yu.A. & N.M. Schmidt (1999) | |
| Zn |
~ 20 meV |
Ga0.47In0.53As; x=0.47 | ||
| Cd |
~ 30 meV |
Ga0.47In0.53As; x=0.47 | ||
| Mn |
~ 50 meV |
Ga0.47In0.53As; x=0.47 | ||
| Fe |
~ 150 meV |
Ga0.47In0.53As; x=0.47 | ||
| (above valence band), 280, 370, and 440 below conduction band |
||||
| Mg |
~ 25 meV |
GaxIn1-xAs; 0<x<1 | ||
| Be |
~ 25 meV |
GaxIn1-xAs; 0<x<1 | ||
| Cd |
~ 8-20 meV |
GaxIn1-xAs; 0<x<1 | ||
| (above valence band), 280, 370, and 440 below conduction band |
||||
| Sn-10; Ge-14; Si-20; Cd-15; Zn-10 meV |
InAs; x=0 | |||
| C - 20, Si - three acceptor levels ~ 30, 100,
and 220, Ge - 30, Zn - 25, Sn - 20. |
GaAs; x=1 | |||