New Semiconductor Materials. Biology systems.
Characteristics and Properties

NSM Archive - Gallium Indium Arsenide Antimonide (GaInAsSb) - Band structure

Band structure and carrier concentration

Basic Parameters
Band structure
Intrinsic carrier concentration
Effective Density of States in the Conduction and Valence Band
Temperature Dependences
Dependences on Hydrostatic Pressure
Band Discontinuities at Heterointerfaces
Effective Masses and Density of States
Donors and Acceptors

---

Basic Parameters for Ga_xIn_1-xAs_ySb1-y

Zinc Blende crystal structure

		Remarks	Referens
Energy gaps, Eg	(0.29 -0.65x+0.6x2) eV	300 K; compositions lattice-matched to GaSb.	Mikhailova M.P. (1999)
	(0.36 -0.23x+0.54x2) eV	300 K; compositions lattice-matched to InAs.
Electron affinity	(4.87 -0.81x) eV	300 K; compositions lattice-matched to GaSb.
	(4.9 -0.83x) eV	300 K; compositions lattice-matched to InAs.
Conduction band
Energy separation between X valley and top of the valence band EX	see Energy separations	300 K; compositions lattice-matched to GaSb and InAs.	Mikhailova M.P. (1999)
Energy separation between L valley and top of the valence band EL	see Energy separations	300 K; compositions lattice-matched to GaSb and InAs.
Effective conduction band density of states	2.5x1019 (0.022+0.03x -0.012x2)3/2 cm-3	300 K; compositions lattice-matched to GaSb.
	2.5x1019 (0.023+0.032x -0.012x2)3/2 cm-3	300 K; compositions lattice-matched to InAs.
Valence band
Energy separation of spin-orbital splitting Eso	see Energy of spin-orbital splitting	300 K; compositions lattice-matched to GaSb.	Mikhailova M.P. (1999)
Effective valence band density of states	2.5x1019 (0.41+0.16x +0.23x2) 3/2 cm-3	300 K; compositions lattice-matched to GaSb.
	2.5x1019 (0.41+0.14x +0.23x2) 3/2 cm-3	300 K; compositions lattice-matched to InAs.
Intrinsic carrier concentration	*** cm-3	300 K

---

Band structure for Ga_xIn_1-xAs_ySb_1-y

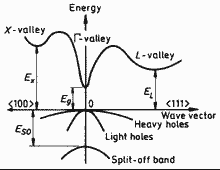	GaxIn1-xAsySb1-y (zinc blende, cubic). Band structure of alloys lattice-matched to InP. Important minima of the conduction band and maxima of the valence band.. For details see Mikhailova M.P. (1999) .
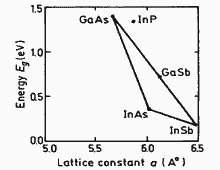	GaxIn1-xAsySb1-y. Energy gap Eg of vs. lattice constant Yakovlev et al.(1988)
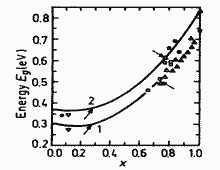	GaxIn1-xAsySb1-y. Energy gap Eg of vs. x for lattice-matched to GaSb. Experimental points are taken from five different source. Arrows show region of miscibility gap. 1 - T= 300 K; 2 - T= 77K. Mikhailova and Titkov (1994)
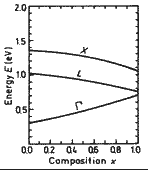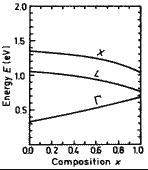
	GaxIn1-xAsySb1-y. Energy separations between G , L and X condition band minima and top of the valence band vs. composition parameter x for lattice-matched to GaSb. Adachi (1987)
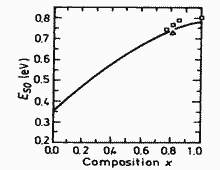
	GaxIn1-xAsySb1-y. Energy separations between G , L and X condition band minima and top of the valence band vs. composition parameter x for lattice-matched to InAs. Adachi (1987)
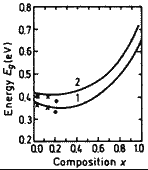
	GaxIn1-xAsySb1-y. Energy of spin-orbital splitting Eso vs. composition parameter x for GaInAsSb lattice-matched to GaSb. Tournie (1990)
	GaxIn1-xAsySb1-y. Energy gap Eg of vs. x for lattice-matched to InAs. 1 - T= 300 K; 2 - T= 77K. Voronina et al.(1991,a)

Within a whole range of the compositions the is a direct gap semiconductor.
For Ga_xIn_1-xAs_ySb1-y compositions lattice-matched to GaSb there is a miscibility gap for 0.25<x<0.75 with a critical temperature estimated to be 1467^oC
(Cherng et al.(1986))
For Ga_xIn_1-xAs_ySb1-y compositions lattice-matched to GaSb :

Eg ~= 0.725x +0.290(1-x) -0.6x(1-x) (eV)	(300K)	Karouta et al.(1987)
Eg ~= 0.801x +0.354(1-x) -0.6x(1-x) (eV)	(77K)
where T is temperature in degrees K

For Ga_xIn_1-xAs_ySb1-y compositions lattice-matched to InAs :

Eg ~= 0.36x -0.23x +0.54x2 (eV)	(300K)	Karouta et al.(1987)
Eg ~= 0.41x -0.29x +0.66x2 (eV)	(77K)
where T is temperature in degrees K

Brillouin zone of the face centered cubic lattice, the Bravais lattice of the diamond and zincblende structures.

Brillouin zone of the hexagonal lattice.

---

Temperature Dependences

The energy gap versus temperature for Ga_xIn_1-xAs_yP_1-y

GaSb (x=1, y=0)	Eg ~= 0.813 - 3.78·10-4xT2/(T+94) (eV)	0 < T < 300	Wu and Chen (1992)
InAs (x=0, y=1)	Eg = 0.415 - 2.76·10-4xT2/(T+83) (eV)		Fang et al. (1990)
Ga0.07In0.93As0.88Sb0.12	Eg ~= 0.378 - 4.27·10-4xT2/(T+288) (eV)		Gong et al. (1994)
	where T is temperature in degrees K

 

---

Lasing wavelength λ₀

Intrinsic carrier concentration:

n_i = (N_c·N_v)^1/2exp(-E_g/(2k_BT))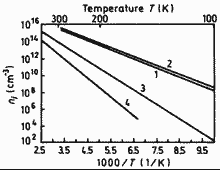

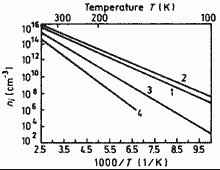
	GaxIn1-xAsySb1-y. Intrinsic carrier concentration vs. temperature for GaxIn1-xAsySb1-y alloys lattice-matched to GaSb. 1 -- x= 0; 2 -- x= 0.2; 3 -- x= 0.8; 3 -- x= 1.0. Mikhailova M.P. (1999)
	GaxIn1-xAsySb1-y. Intrinsic carrier concentration vs. temperature for GaxIn1-xAsySb1-y alloys lattice-matched to InAs. 1 -- x= 0; 2 -- x= 0.2; 3 -- x= 0.8; 3 -- x= 1.0. Mikhailova M.P. (1999)

Effective density of states in the conduction band: N_c

N_c ~= 4.82 x 10¹⁵ · (m_Γ/m₀)^3/2T^3/2 (cm^-3) ~= 4.82 x 10¹⁵ · (0.022 +0.03x -0.012x²)^3/2 T^3/2 (cm^-3) :
(for GaInAsSb alloys lattice-matched to GaSb)

N_c ~= 4.82 x 10¹⁵ · (m_Γ/m₀)^3/2T^3/2 (cm^-3) ~= 4.82 x 10¹⁵ · (0.023 +0.032x -0.012x²)^3/2 T^3/2 (cm^-3) :
(for GaInAsSb alloys lattice-matched to InAs)

Effective density of states in the valence band: N_v

N_v ~= 4.82 x 10¹⁵ · (m_h/m₀)^3/2 T^3/2 (cm^-3)= 4.82 x 10¹⁵ · (0.41 +0.16x +0.23x²)^3/2 T^3/2 (cm^-3) :
(for GaInAsSb alloys lattice-matched to GaSb)

N_v ~= 4.82 x 10¹⁵ · (m_h/m₀)^3/2 T^3/2 (cm^-3)= 4.82 x 10¹⁵ · (0.41 +0.14x +0.23x²)^3/2 T^3/2 (cm^-3) :
(for GaInAsSb alloys lattice-matched to InAs)

---

Dependence on Hydrostatic Pressure

---

Band Discontinuities at Heterointerfaces

at GaInAsSb/GaSb and GaInAsSb/InAs heterojunctions.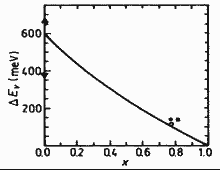

	GaxIn1-xAsySb1-y. Valence band discontinuity offset ΔEv vs. concentration x for lattice-matched GaxIn1-xAsySb1-y/GaSb heterostructure. Mebarki et al. (1993)
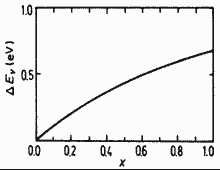	GaxIn1-xAsySb1-y. Valence band discontinuity offset ΔEv vs. concentration x for lattice-matched GaxIn1-xAsySb1-y/InAs heterostructure. Nakao et al. (1984)
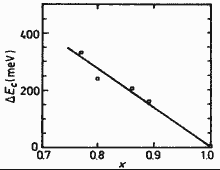	GaxIn1-xAsySb1-y. Conduction band discontinuity offset ΔEc vs. concentration x for lattice-matched GaxIn1-xAsySb1-y/GaSb heterostructure. Mikhailova M.P. & Titkov (1994)

---

Effective Masses and Density of States:

Electrons

Effective Electron Masses		Remarks	Referens
Effective electron mass me	0.022+0.03x -0.012x2 mo	300K; for GaInAsSb lattice-matched to GaSb	Mikhailova M.P. (1999)
	0.023+0.032x -0.012x2 mo	300K; for GaInAsSb lattice-matched to InAs

Holes

		Remarks	Referens
Effective mass of density of states mv	mv ~= 0.41 +0.16x +0.023x2 mo	300K; for GaInAsSb lattice-matched to GaSb	Mikhailova M.P. (1999)
	mv ~= 0.41 +0.14x +0.023x2 mo	300K; for GaInAsSb lattice-matched to InAs

Donors and Acceptors

Undoped Ga_xIn_1-xAs_ySb1-y compositions ( 0 < x < 0.2 ) have the conductivity of p-type .
Three native acceptor traps have been observed for these compositions :
E_t -E_v 0.01 eV
(E_c -E_v) ~= 0.03--0.035 eV
(E_t -E_v) ~= 0.07 eV
Undoped Ga_xIn_1-xAs_ySb1-y compositions ( 0.76 <x < 1 ) have the conductivity of n-type.

Ionization energies of Shallow Donors			Remarks
Te     (donor)	Ec -Et	~ 5x10-3 eV	GaxIn1-xAsySb1-y (0 < x <0.2)	Baranov et al.(1990), Voronina et al.(1991,b)
	Ec -Et	0.04 -- 0.05 eV	GaxIn1-xAsySb1-y (0 < x <0.2)	Baranov et al.(1990), Voronina et al.(1991,b)
	Ec -Et	0.09 -- 0.1 eV	GaxIn1-xAsySb1-y (0.8 < x)	Voronina et al.(1991,a)
Ionization energies of Shallow Acceptor
Ge, Cd   (acceptor)	Et -Ev	~ 0.01 eV	GaxIn1-xAsySb1-y (0 < x <0.2)	Baranov et al.(1990), Voronina et al.(1991,b)
Ge +Vac(acceptor)	Et -Ev	~ 0.017 eV	GaxIn1-xAsySb1-y (0 < x <0.2)	Baranov et al.(1990), Voronina et al.(1991,b)
Cd +Vac (acceptor)	Et -Ev (acceptor)	~ 0.017 eV	GaxIn1-xAsySb1-y (0 < x <0.2)	Baranov et al.(1990), Voronina et al.(1991,b)
Zn (acceptor)	Et -Ev	~ 0.1 -- 0.15 eV	GaxIn1-xAsySb1-y (0 < x <0.2)	Baranov et al.(1990), Voronina et al.(1991,b)
Mn	Et -Ev	~ 0.02 -- 0.25 eV	GaxIn1-xAsySb1-y (0.8 < x)	Voronina et al.(1991,a)

 

Statistics