New Semiconductor Materials. Biology systems.
Characteristics and Properties

NSM Archive - Gallium Indium Arsenide Phosphide (GaInAsP) - Band structure

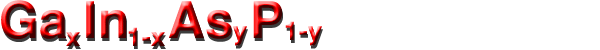
Band structure and carrier concentration

Basic Parameters
Band structure
Intrinsic carrier concentration
Lasing wavelength
Effective Density of States in the Conduction and Valence Band
Temperature Dependences
Dependences on Hydrostatic Pressure
Band Discontinuities at Heterointerfaces
Effective Masses and Density of States
Donors and Acceptors

---

Basic Parameters for Ga_xIn_1-xAs_yP_1-y

Zinc Blende crystal structure

Energy gaps, Eg	0.354(InAs) ÷2.27(GaP) eV	300 K
Direct energy gaps, Eg     min     max	0.354 (InAs)     2.17
Direct energy gaps composition, Eg	1.35 +0.668x -1.068y +0.758x2 +0.078y2 -0.069xy -0.332x2y +0.03xy2 eV	300 K
	Ga0.47In0.53AsyP1-y	Remarks	Referens
Energy gaps, Eg	(1.344-0.738y+0.138y2) eV	300 K	Goldberg Yu.A. & N.M. Schmidt (1999)
Electron affinity	##### eV	300 K
Conduction band
Energy separation between X valley and top of the valence band EX;	(2.19-0.86y) eV	300 K	Goldberg Yu.A. & N.M. Schmidt (1999)
Energy separation between L valley and top of the valence band EL	(1.93-0.73y) eV	300 K
Effective conduction band density of states	2.5x1019 (0.08-0.039y)3/2 cm-3	300 K
Valence band
Energy separation of spin-orbital splitting Eso	(0.11+0.24y) eV	300 K
Effective valence band density of states	2.5x1019 (0.6-0.18y)3/2 cm-3	300 K
Intrinsic carrier concentration	4.3 x 108 cm-3 (for y=0.27) 4.4 x 109 cm-3 (for y=0.47) 6.7 x 1011 cm-3 (for y=1.0)	300 K

---

Band structure for Ga_xIn_1-xAs_yP_1-y

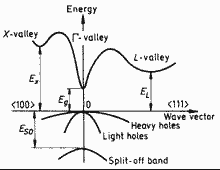	GaxIn1-xAsyP1-y (zinc blende, cubic). Band structure of alloys lattice-matched to InP. Important minima of the conduction band and maxima of the valence band.. For details see Goldberg Yu.A. & N.M. Schmidt (1999) .
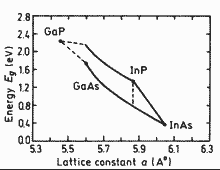	+Energy gap Eg of vs. lattice constant Solid lines represent direct band region. Dashed lines represent indirect band region Foyt (1991) For direct band region (300K): Eg = 1.35+0.68x -1.068y +0.758x2+ 0.78y2 -0.069 xy -0.332 x2y +0.3 xy2, (eV)
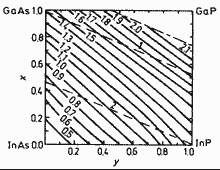	GaxIn1-xAsyP1-y. Energy gap Eg of vs. x and y. 300K Dashed lines represent the compositions lattice- matched to GaAs (1) and InP (2) Gorelenok et al. (1981)
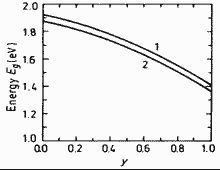	GaxIn1-xAsyP1-y. Energy gap Eg of vs. concentration y for lattice-matched. 300K 1 -- GaAs; 2 -- ZnSe Adachi (1982)
	GaxIn1-xAsyP1-y. Energy gap Eg of vs. x and y. 300K Dashed lines represent the compositions lattice- matched to GaAs (1) and InP (2) Gorelenok et al. (1981)

For direct band region (300K):
E_g = 1.35 +0.68x -1.068y +0.758x²+ 0.078y² -0.069 xy -0.332 x²y +0.3 xy², (eV)
For compositions lattice-matched to InP (300K):
E_g = 1.344 -0.738y +0.138 y² , (eV)
For compositions lattice-matched to InP (4.2K):
E_g = 0.41(1-x)y +1.42(1-x)(1-y)+ 1.51xy +2.34x(1-y) -0.54x(1-x) -0.17y(1-y) = 1.42 - y +0.37 y², (eV)
Benzaquen et al.(1994)

Brillouin zone of the face centered cubic lattice, the Bravais lattice of the diamond and zincblende structures.

Brillouin zone of the hexagonal lattice.

---

Temperature Dependences

The energy gap versus temperature for Ga_xIn_1-xAs_yP_1-y lattice-matched
to InP :

Eg = Eg(0) - 4.3·10-4x T2/(T + 224)	(eV)	Satzke et al. (1988)
Eg(0) = **** eV
where T is temperature in degrees K

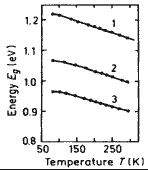GaxIn1-xAsyP1-y. Energy gap Eg of vs. temperature for three compositions lattice-matched to InP. 1 -- y=0.3; 2 -- y=0.48; 3 -- y=0.69. Yamazoe et al. (1981)

---

Lasing wavelength λ₀

Lasing wavelength λ₀ versus temperaturefor GaInAsP/InP double-hetero-structure lasers:

dλ0/dt ~= 4A/K	at dλ0=1.3 μm	(y=0.6)	Arai et al.(1980)
dλ0/dt ~= 5A/K	at dλ0=1.55μm	(y=0.9)

Intrinsic carrier concentration:

n_i = (N_c·N_v)^1/2exp(-E_g/(2k_BT))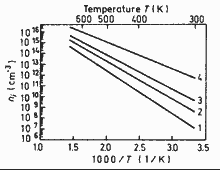

GaxIn1-xAsyP1-y. Intrinsic carrier concentration vs. temperature for GaxIn1-xAsyP1-y alloys lattice-matched to InP. 1 -- y= 1; 2 -- y= 0.47; 3 -- y= 0.27; 3 -- y= 0.0. Yamazoe et al. (1981)

Effective density of states in the conduction band: N_c

N_c ~= 4.82 x 10¹⁵ · (m_Γ/m₀)^3/2T^3/2 (cm^-3) ~= 4.82 x 10¹⁵ · (0.08-0.039)^3/2 T^3/2 (cm^-3) :
(for GaInAsP alloys lattice-matched to InP)

Effective density of states in the valence band: N_v

N_v ~= 4.82 x 10¹⁵ · (m_h/m₀)^3/2 T^3/2 (cm^-3)= 4.82 x 10¹⁵ · (0.6-0.18y)^3/2 T^3/2 (cm^-3)
(for GaInAsP alloys lattice-matched to InP)

---

Dependence on Hydrostatic Pressure

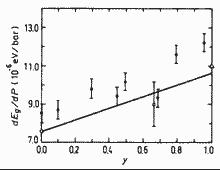GaxIn1-xAsyP1-y. Hydrostatic-pressure coefficient dependence of the energy gap Eg vs. concentration y for Adachi (1992)

---

Band Discontinuities at Heterointerfaces

GaInAsP/InP			Referens
Conduction band discontinuity	ΔEc = 268y+3y2 meV	77K	Adachi (1992)
Valence band discontinuity	ΔEv = 0.7 eV	77K
Band discontinuities at Ga0.47In0.53As and Al0.48In0.52As heterojunction
Conduction band discontinuity	ΔEc = 520 meV	300K	see also Adachi (1992)

The conduction-band discontinuities DEc versus band-gap
differences DEg between
composition and InP for GaInAsP/InP
heterojunctions. 300K.
(after Forrest et al.(1984)).

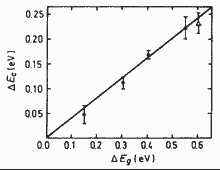GaxIn1-xAsyP1-y. Conduction band discontinuity ΔEc vs. band-gap differences ΔEg between GaxIn1-xAsyP1-y composition and InP heterojunctions. 300K Forrest et al.(1984)

---

Effective Masses and Density of States:

Electrons

For wurtzite crystal structure the surfaces of equal energy in Γ valley should be ellipsoids, but effective masses in z direction and perpendicular directions are estimated to be approximately the same:

Effective Electron Masses		Remarks	Referens
Effective electron mass me	0.08-0.05y+0.017y2 mo~= ~=0.08-0.039y mo	Ga0.47In0.53AsyP1-y; 300K for alloys lattice-matched to InP	Goldberg Yu.A. & N.M. Schmidt (1999)

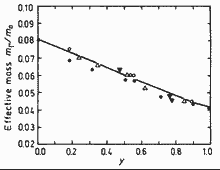	GaxIn1-xAsyP1-y. Electron effective mass in GaInAsP alloys vs. concentration y for compositions lattice-matched to InP 300K Pearsall (1982
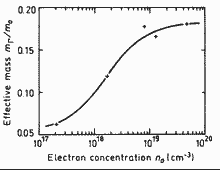	GaxIn1-xAsyP1-y. Electron effective mass in Ga0.1In0.9As0.3P0.7 alloys vs. electron concentration 80K Vilkotsky et al.(1986)

Holes

Effective Masses for Zinc Blende GaN		Remarks	Referens
Effective hole masses (heavy) mh	mh ~= (0.6 -0.18y) mo	Ga0.47In0.53AsyP1-y; 300K	Goldberg Yu.A. & N.M. Schmidt (1999)
Effective hole masses (light) mlp	mlp ~= (0.12 -0.099y +0.03y 2) mo	Ga0.47In0.53AsyP1-y; 300K
Effective hole masses (split-off band) ms	mso ~= (0.21 -0.01y -0.05y 2) mo	Ga0.47In0.53AsyP1-y; 300K

Donors and Acceptors

For composition alloys lattice-matched to InP:

Ionization energies of Shallow Donors		Remarks
Sn, Ge, Si, Te, S	~ 3 meV		Goldberg Yu.A. & N.M. Schmidt (1999)
Ionization energies of Shallow Acceptor
Mg	~ 35 meV		Goldberg Yu.A. & N.M. Schmidt (1999)
Zn	37.5-22 eV	for  y=0.3-0.9
Cd	~ 60-30 meV	for  y=0.2-0.9
Be	~ 40 meV

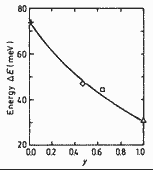	GaxIn1-xAsyP1-y. Ionization energy of Cd vs. concentration y y for GaInAsP alloys lattice-matched to InP Wehmann et al.(1986)
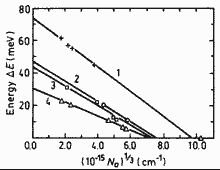	GaxIn1-xAsyP1-y. Ionization energy of Cd vs. acceptor concentration Na for four GaInAsP alloys lattice-matched to InP 77K 1 - y=0 (InP); 2 - y=0.47; 3 - y=0.64; 4 - y=1 Wehmann et al.(1986)

 

Statistics