New Semiconductor Materials. Biology systems.
Characteristics and Properties

Band structure and carrier concentration of Gallium Arsenide (GaAs)

Band structure and carrier concentration

Basic Parameters
Temperature Dependences
Dependence of the Energy Gap on Hydrostatic Pressure
Energy Gap Narrowing at High Doping Levels
Effective Masses
Donors and Acceptors

Basic Parameters

Energy gap	1.424 eV
Energy separation (EΓL) between Γ and L valleys	0.29 eV
Energy separation (EΓX) between Γ and X valleys	0.48 eV
Energy spin-orbital splitting	0.34 eV
Intrinsic carrier concentration	2.1·106 cm-3
Intrinsic resistivity	3.3·108 Ω·cm
Effective conduction band density of states	4.7·1017 cm-3
Effective valence band density of states	9.0·1018 cm-3

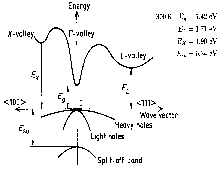Band structure and carrier concentration of GaAs. 300 K Eg = 1.42 eV EL = 1.71 eV EX= 1.90 eV Eso = 0.34 eV

Temperature Dependences

Temperature dependence of the energy gap

E_g=1.519-5.405·10^-4·T²/(T+204) (eV)
where T is temperatures in degrees K (0 < T < 10³).

Temperature dependence of the energy difference between the top of the valence band and the bottom of the L-valley of the conduction band

E_L=1.815-6.05·10^-4·T²/(T+204) (eV)

Temperature dependence of the energy difference between the top of the valence band and the bottom of the X-valley of the conduction band

E_L=1.981-4.60·10^-4·T²/(T+204) (eV)

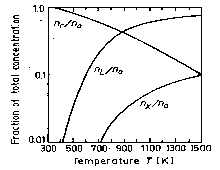	The temperature dependences of the relative populations of the Γ, L and X valleys. (Blakemore [1982]).
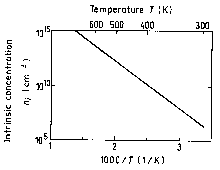	The temperature dependences of the intrinsic carrier concentration. (Shur [1990]).

Intrinsic Carrier Concentration

n_i =(N_c ·N_ν )^1/2exp(-E_g/(2k_bT))

Effective density of states in the conduction band taking into account the nonparabolicity of the Γ-valley and contributions from the X and L-valleys
N_c= 8.63·10¹³·T^3/2[1-1.9310^-4·T-4.19·10^-8·T² +21·exp(-E_ΓL/(2k_bT)) +44·exp(-E_ΓX/(2k_bT)) (cm^-3)

Effective density of states in the valence band

N_v= 1.83·10¹⁵·T^3/2(cm^-3)

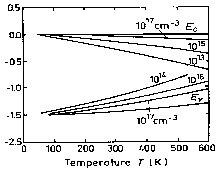Fermi level versus temperature for different concentrations of shallow donors and acceptors.

Dependences on Hydrostatic Pressure

E_g = E_g(0) + 0.0126·P - 3.77·10^-5P² (eV)
E_L = E_L(0) + 5.5·10^-3P (eV)
E_X = E_X(0) + 1.5·10^-3P (eV)
where P is pressure in kbar.

Energy Gap Narrowing at High Doping Levels

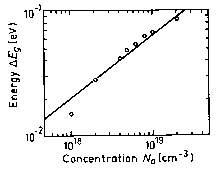Energy gap narrowing at high doping levels. (Tiwari and Wright [1990])

ΔEg ≈ 2·10^-11·N_a^-1/2 (eV) (N_a- in cm.^-3)

Effective Masses

Electrons:

For Γ-valley	mΓ = 0.063mo
In the L-valley the surfaces of equal energy are ellipsoids
	ml= 1.9mo
	mt= 0.075mo
Effective mass of density of states
mL=(16mlmt2)1/3	mL=0.85mo
In the X-valley the surfaces of equal energy are ellipsoids
	ml= 1.9mo
	mt= 0.19mo
Effective mass of density of states
mX=(9mlmt2)1/3	mX=0.85mo

Holes:

Heavy	mh = 0.51mo
Light	mlp = 0.082mo
Split-off band	mso = 0.15mo
Effective mass of density of states	mv = 0.53mo

Donors and Acceptors

Ionization energies of shallow donors (eV)
(Milnes [1973])

S	Se	Si	Ge	Sn	Te
~0.006	~0.006	~0.006	~0.006	~0.006	~0.03

Ionization energies of shallow acceptors (eV)
(Milnes [1973])

C	Si	Ge	Zn	Sn
~0.02	~0.03/0.1/0.22	~0.03	~0.025	~0.2

 

Statistics